
For the purpose of constructing the diagram in Figure 2.15.3 the base temperature is taken as 273 K not 273.15 K.īy assuming a kilogram of water at atmospheric pressure, and by adding 4.228 kJ of energy, the water temperature would rise by 1 K from 273 K to 274 K. The specific heat of saturated water at this temperature is 4.228 kJ/kg K. As entropy is measured in terms of absolute temperature, the origin temperature of 0 ☌ is taken as 273.15 K. By starting at the origin of the graph at a temperature of 0 ☌ at atmospheric pressure, and by adding enthalpy in small amounts, the graph can be built. To produce such a diagram, the entropy values can be calculated. The area to the right of the dry saturated steam line is the superheated steam region, and lines of constant pressure now curve upwards as soon as they cross the dry saturated steam line.Ī variation of the diagram in Figure 2.15.2, that can be extremely useful, is one in which the horizontal axis is not enthalpy but instead is enthalpy divided by the mean temperature at which the enthalpy is added or removed. The horizontal distance between the saturated water line and the dry saturated steam line represents the amount of latent heat or enthalpy of evaporation, and is called the evaporation line (enthalpy of evaporation decreases with rising pressure). Lines of constant pressure originate on the saturated water line. Since the temperature and pressure at which water boils are in a fixed relationship to each other, Figure 2.15.1 could equally be drawn to show enthalpy against temperature, and then turned so that temperature became the vertical ordinates against a base of enthalpy, as in Figure 2.15.2. To see how this works, perhaps it is best to start off with a diagram showing how the enthalpy content of a kilogram of water increases as it is heated to different pressures and evaporated into steam. A more practical approach is to define entropy as energy added to or removed from a system, divided by the mean absolute temperature over which the change takes place. That may be of some philosophical interest, but does not help very much in the calculation of actual values. The increase of entropy in the overall system always takes place in the same direction as time flows. If the entropy of a system is calculated at two different conditions, then the condition at which the entropy is greater occurs at a later time. This compulsion to spread out has led some observers to label entropy as ‘time’s arrow’.

It is, in some ways, a measure of the lack of quality or availability of energy, and of how energy tends always to spread out from a high temperature source to a wider area at a lower temperature level. Entropy values can then be listed and used in calculations in particular, calculations to do with steam flow, and the production of power using turbines or reciprocating engines.

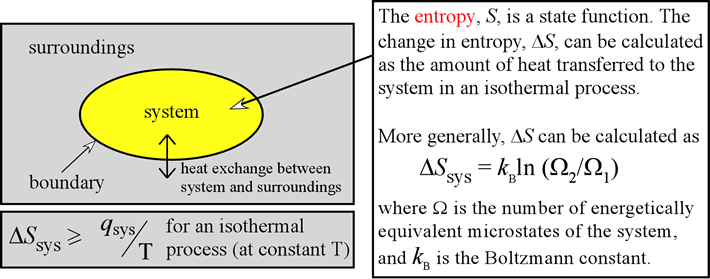
Rather, it must be calculated from things that can be measured. A sensor cannot detect it, and it does not show on a gauge. When entropy increases, a certain amount of energy becomes permanently unavailable to do work.In some ways, it is easier to say what it is not! It is not a physical property of steam like pressure or temperature or mass. Entropy is associated with the unavailability of energy to do work. In the second case, entropy is greater and less work is produced. The same heat transfer into two perfect engines produces different work outputs, because the entropy change differs in the two cases. There is 933 J less work from the same heat transfer in the second process. We noted that for a Carnot cycle, and hence for any reversible processes, We can see how entropy is defined by recalling our discussion of the Carnot engine.

That unavailable energy is of interest in thermodynamics, because the field of thermodynamics arose from efforts to convert heat to work. Although all forms of energy are interconvertible, and all can be used to do work, it is not always possible, even in principle, to convert the entire available energy into work. Entropy is a measure of how much energy is not available to do work. Recall that the simple definition of energy is the ability to do work. Making Connections: Entropy, Energy, and Work


 0 kommentar(er)
0 kommentar(er)
